How to Compensate Pressure Changes in Temperature Control

Related Vendors

DÜPERTHAL Sicherheitstechnik GmbH & Co. KG

Analysis: As explained above, in the current scenario, Antoine’s equation for pure component is applied to the mixture of hydrocarbons. Vapour pressure and corresponding saturation temperature data for the tray composition is required to determine the coefficients of the equation. Here, since the temperature transmitter is located on the first tray, bottom product composition is considered for calculations. Since this is a grass root set up and no operating data is available, the required bubble point - pressure data is generated for the bottom product composition using Pro-II (table 2) simulation.

The Effect of Steam Pressure on Temperature Control

Effect of changes in Deisobutanizer column pressure on temperature is studied. It is observed from table 2 that column temperature may vary by about 70C i.e. from 121 to 1280C even if pressure varies by (+/-) 0.5 Kg/cm2 from operating pressure. The pressure variations could disturb the column temperature control system. Thus pressure compensation is essential to nullify the effect of pressure change.

Antoine’s equation is given by

ln P = A - B / (T + C) (1)

Antoine’s equation is linearized to eq. 2

ln P = A + (AC-B) / T - C (ln P)/T (2)

Coefficients of the above equation are determined using multivariable linear regression data analysis tool of MS Excel 2010. Antoine’s equation can be re-written in the form mentioned below

Controlling process parameters is vital to satisfactory operation of critical fractionators
(Source: Aker Solutions)

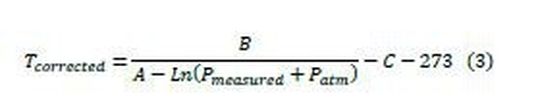
Where,

Patm = Atmospheric PressurePmeasured = Measured column Pressure (kg/cm2g)Tcorrected = Saturation Temperature corresponding to Pmeasured (0C)

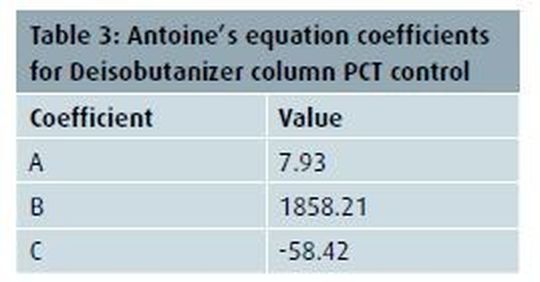
Results: Equation 3 is used to get corrected temperature after pressure compensation. Temperature controller compares this corrected temperature with actual measured temperature and takes corrective action. The values of the coefficients of the equation are calculated and mentioned in table 3.

Table 3: Antoine’s equation coefficients for Deisobutanizer column PCT control
(Source: Aker Solutions)

(ID:38049620)